"Fortune's Formula": Using The Kelly Formula To Be A Better Speculator (And Bettor)
As a speculator – there’s three important steps to ensure maximizing your wealth overtime. . .
First – find situations where you have an edge (an attractive investment you have an advantage in).
Second – invest your bankroll properly (position sizing).
And third – never blow yourself up.
I’ve written many times before about the ‘mental tools’ that help speculators find an edge. Like using Expected Value Analysis (EVA) to make better contrarian bets. Or why ‘second-level thinking’ is important. Or how to spot and exploit favorable optionality.
I’ve also written many times before about the hazards of blowing up. And why this must be avoided at all cost (i.e. avoid negatively asymmetric scenarios - where risks far outweigh any potential gain).
But - I haven’t touched much on investing your bankroll properly (position sizing). . .
Putting it simply – position sizing refers to allocating the optimal amount of capital in each investment (bet).
For instance: two hedge funds with the same amount of capital and same list of stocks can generate very different results - simply based on how they invest their capital.
Great speculators know that it’s not about just finding an attractive play. But how can they make the most money from it.
Like Charlie Munger – considered Warren Buffet’s smarter-half – said: “The wise ones bet heavily when the world offers them that opportunity. They bet big when they have the odds. And the rest of the time, they don’t. It’s just that simple…”
Now – a speculator shouldn’t put all their money in a single play (even if there's a large edge). But they also shouldn’t under-invest. Or worse - over-diversify.
What to do?
Well – that’s where the Kelly-Criterion (aka the Kelly Formula) comes in. . .
Long story short: in 1956, a former Bell Labs (now owned by Nokia) employee – John Kelly - used 'information theory' to create an ideal betting formula.
Kelly wanted to calculate the optimal amount of capital to allocate on a favorable bet given fixed odds.
There are many ways to express the Kelly Formula. But a simplified version of it from value investor Mohnish Pabrai’s book - ‘The Dhandho Investor’ - is:
Edge / Odds = Fraction of Capital That Should Be Allocated (aka E/O = F)
What does all this mean?
An Edge is the total expected value of the bet.
And the Odds are what the market’s offering if you win.
Then – once you calculate the edge and the market’s odds – you determine how much of your bankroll to invest.
Here's an example – imagine having $1,000 dollars in your pocket and you’re walking around a Las Vegas casino.
You spot an empty table that’s playing a coin game where each flip offers two dollars ($2) for heads. But with each tail you lose one dollar (-$1).
It’s not hard to see the opportunity here. Meaning - each toss has a 50-50 chance of heads or tail, but the market's offering 2-to-1 odds for landing on heads.
(Remember – many believe that markets are totally efficient – thus there’s no edge and the odds perfectly represent the probabilities of success. Meaning – in the market's eyes – there’s zero expected value).
So - using Kelly’s Formula – you find the edge is $0.50 cents (aka the expected value; the math for this is 50% x $2 + 50% x -$1).
And the odds are $2 (the amount the market’s offering each time you land heads).
Thus - the fraction (amount) of your capital that should be allocated with each coin toss is 25%. (Mathematically it’s $0.50/$2.00 = 25%).
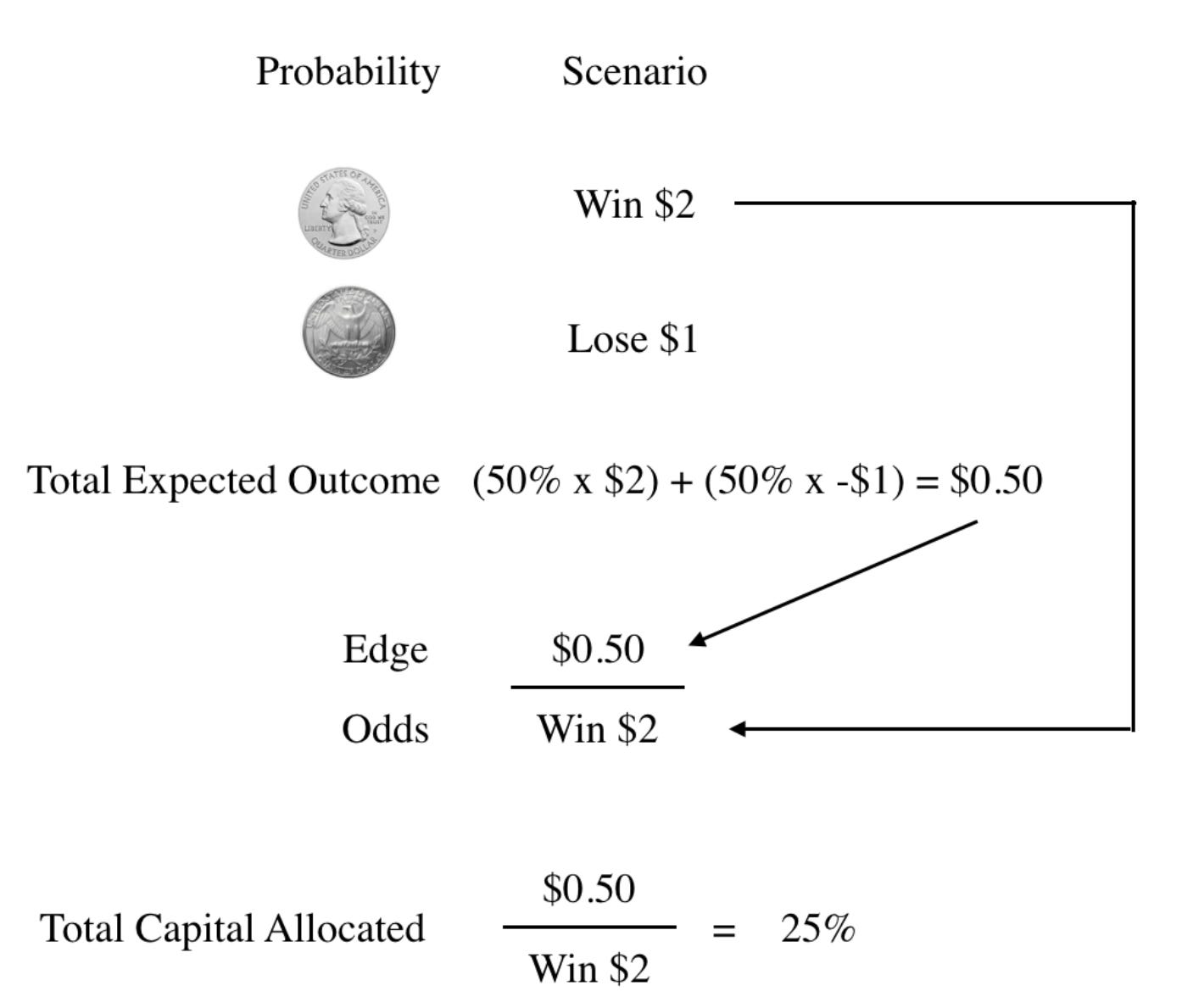
Or - said otherwise – it’s best to bet $250 with each coin flip (since you have a $1,000 bankroll).
And according to Kelly – as long as the edge and odds stay the same - this is the optimal strategy for maximizing wealth in the long-term while playing this game.
Now – at the time – not many traders adopted the Kelly Formula (most likely because efficient market hypothesis was very big back then).
But - one trader discovered this formula. And used it to beat the market by 20% for three decades. . .
I’m talking about Edward O. Thorp. (He was the original ‘quant’ trader and created his own option-pricing model long before the Black-Scholes-Merton option model existed. His auto-biography - ‘A Man of All Markets’ - is a must read in the Speculators Anonymous Reading List).
Here’s what Thorp had to say about the Kelly Formula in the book ‘Hedge Fund Market Wizards’:
“… The Kelly criterion is the bet size that will produce the greatest expected growth rate in the long term. If you can calculate the probability of winning on each bet or trade and the ratio of the average win to average loss, then the Kelly criterion will give you the optimal fraction to bet so that your long-term growth rate is maximized…”
Now – although the Kelly Formula’s a very important tool (one that I use constantly). It still has some issues.
For starters – it was created for gambling. Not the markets.
Secondly - in the market - it’s up to the speculator to determine what they believe the edge is. (The best they can do is estimate).
Thus – for market trading – here’s another version of the Kelly Formula that works well (according to Macro-Ops). . .

Also – like Thorp – the speculator should use the Kelly Formula as a reference point.
For example – if the formula states to invest 20% of your bankroll – you can use ‘half-Kelly’ or ‘quarter-Kelly’. (Meaning cut the 20% in half, or by a quarter, etc).
This helps speculators who are uncertain about their edge. Or want to be more conservative.
Thus - in summary - I believe the Kelly Formula's very useful. And that it belongs in a speculator's 'mental toolbox'.
It isn't perfect (the formula's only as good as its inputs) - but it does have practical use in the markets (as Ed Thorp's proven).
Position sizing's a very important (yet often not talked about) part when placing trades. Especially when the speculator has an edge.
For instance - finding a positively asymmetric (low risk - high reward) opportunity is only half the task. The other half is figuring out how to size the position properly (over-investing can be ruinous, but under-investing won't maximize portfolio returns).
This is why the Kelly-Formula's so important. And why I always use it.
Also - for those that aren't the best mathematicians - don't worry. Here's an easy to use Kelly-Calculator. All that's needed are the inputs.
Thus - keep the Kelly Formula in mind next time you're about to place a trade or a bet. . .
PS - here's a must-read piece about the Kelly Formula written by Michael Mauboussin (one of my favorite economists).
PPS - there's an entire book written about the history and use of the Kelly Formula. It's called "Fortune's Formula: The Untold Story of the Scientific Betting System That Beat the Casinos and Wall Street' - by William Poundstone. I highly recommend it.



